Lektion 28
Bezier Flächen (Bezier Patches)
Geschrieben von: David Nikdel ( ogapo@ithink.net )
Dieses Tutorial soll Sie in Bezier Flächen einführen, in der Hoffnung, dass jemand der künstlerisch mehr begabt als ich ist, etwas ziemlich cooles damit macht und es uns zeigt. Es ist nicht als eine komplette Bezier Patch Bibliothek beabsichtig, sondern viel mehr als Einstiegspunkt, um Sie damit vertraut zu machen, wie gekrümmte Oberflächen arbeiten. Außerdem, da dies hier nur zu Information dient, habe ich nicht die ganz korrekte Terminologie zugunsten des Verständnisses benutzt; Ich hoffe, dass jeder damit einverstanden ist. Für jeden, der bereits mit Beziers vertraut ist und das hier nur liest, um zu sehen, ob ich es verhunzt habe: schämen Sie sich ;-), aber wenn Sie etwas völlig falsches finden, lassen sie es mich oder NeHe wissen, da ja keiner perfekt ist, oder nicht? Oh, noch eine weitere Sache: der komplette Code wurde in keinster Weise über meinen normalen Programmierstil hinaus optimiert. Ich möchte, dass jeder genau weiß, was vorgeht. Nun denn, ich denke das ist genug zur Einführung. Auf geht's!
Die Mathematik - ::dämonische Musik:: (achtung, etwas längerer Abschnitt)
Ok, es dürfte recht schwierig sein Beziers zu verstehen, ohne die grundlegendsten Verständnisse der Mathematik, die dahinter steht, wie dem auch sei, wenn Sie diesen Teil gerade nicht lesen wollen oder Sie bereits die Mathematik kennen, können Sie diesen Teil überspringen. Ich werde mit der Beschreibung beginnen, was eine Bezier Kurve ist und dann dahin übergehen, wie man ein Bezier Patch erzeugt.
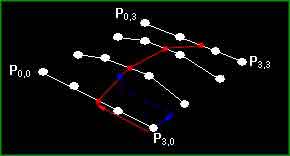
Komisch ist, dass, wenn Sie jemals ein Graphic-Programm verwendet haben, Sie bereits mit Bezier Kurven vertraut sind, wenn auch wahrscheinlich nicht unter diesem Namen. Sie sind die verbreitetste Methode um krumme Linien zu zeichnen und werden in der Regel durch eine Reihe von Punkten repräsentiert, wobei jeder 2 Punkte hat, die die Tangente repräsentieren, am Punkt links und rechts davon. So sieht das aus:
Das ist die einfachst mögliche Bezier Kurve (längere werden durch viele kleine gebildet (häufig ohne dass der Benutzer es merkt)). Diese Kurve ist tatsächlich nur durch 4 Punkte definiert, das wären die 2 End-Kontroll-Punkte und die 2 mittleren Kontroll-Punkte. Für den Computer sind alle Punkte gleich, aber um uns das Designen zu erleichtern verbinden wir jeweils die ersten und letzten zwei, da diese immer Tangenten zum Endpunkt sind. Die Kurve ist eine parametrische Kurve und wird gezeichnet, indem Punkte, die direkt auf der Kuve liegen, mit geraden Linien verbunden werden. Auf diesem Weg können Sie die Auflösung des Patch kontrollieren (und den rechen Aufwand). Der gebräuchlichste Weg ist es bei höherer Entfernung weniger Details zu verwenden und je näher der Betrachter kommt, entsprechend mehr, so dass es immer nach einer perfekt gekrümmten Oberfläche aussieht, mit dem geringsten Rechenaufwand.
Bezier Kurven basieren auf einer Basis-Funktion, von der kompliziertere Versionen abgeleitet werden. Hier die Funktion:
t + (1 - t) = 1
Klingt einfach, was? Nunja, ist es auch, das ist die einfachste Bezier Kurve, eine Kurve ersten Grades. Wie Sie vielleicht aus der Terminologie erkennen können, handelt es sich bei Bezier Kurven um Polynome und wie wir uns aus der Algebra erinnen, ein Polynom ersten Grades ist einfach nur eine gerade Linie; nicht gerade interessant. Nun, da die Basis-Funktion für alle Nummer t wahr ist, können wir quadrieren, sie in die dritte Potenz erheben, was auch immer, es würde immer noch wahr sein, richtig? Versuchen wir's mit der dritten Potenz.
(t + (1-t))^3 = 1^3
t^3 + 3*t^2*(1-t) + 3*t*(1-t)^2 + (1-t)^3 = 1
Das ist die Gleichung die wir benutzen werden, um das gängiste Bezier zu berechnen, die Bezier Kurve dritten Grades. Sie ist am gängisten für zwei Gründe, a) es ist das Polynomal des kleinsten Grades, das nicht notwendigerweise in einer Ebene lieben muss (es gibt 4 Kontrollpunkte) und b) die Tangenten Linien an den Seiten sind nicht voneinander abhängig (bei 2ten Grades gäbe es nur 3 Kontrollpunkte). Sehen Sie bereits die Bezier Kurve? Hehe, ich auch nicht, deshalb muss ich eine Sache noch hinzufügen.
Ok, da die gesamte linke Seite gleich 1 ist, ist es sicher anzunehmen, dass wenn Sie alle Komponenten addieren, Sie immer noch gleich 1 sind. Hört sich das danach, ob wir damit entscheiden können, wieviel jeder Kontrollpunkt benutzt wird, um einen Punkt in der Kurve zu berechnen? (hinweise: sagen Sie einfach ja ;-) ) Sie haben recht! Wenn wir den Wert eines Punktes einige Prozent entlängs der Kurve berechnen wollen, multiplizieren wir einfach jeden Teil mit einem Kontrollpunkt (als Vektor) und finden die Summe. Generell kann man sagen, wir arbeiten mit 0
P1*t^3 + P2*3*t^2*(1-t) + P3*3*t*(1-t)^2 + P4*(1-t)^3 = Pneu
Da Polynome immer stetig sind, ist das ein guter Weg, um zwischen den 4 Punkten zu morphen. Die einzigen Punkte die tatsächlich erreicht werden, sind P1 und P4 wenn t = 1, bzw. gleich 0 ist.
Nun, das ist alles schön und gut, aber wie kann ich das in 3D verwenden werden Sie sich fragen. Nun, eigentlich ist es recht einfach, um eine Bezier Patch zu formen, brauchen Sie 16 Kontrollpunkte (4*4) und 2 Variablen t und v. Daraus berechnen Sie ein Punkte bei v entlängs der 4 parallelen Kurven, dann benutzen Sie diese 4 Punkte um eine neue Kurve zu machen und berechnen t entlängs dieser Kurve. Indem wir genügend dieser Punkte berechnen, können wir Triangle Strips zeichnen und diese miteinander verbinden, woraus unser Bezier Patch ensteht.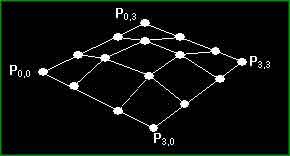
Ich denke das war erst mal genug Mathe für jetzt, auf zum Code!#include <windows.h> // Header Datei für Windows #include <math.h> // Header Datei für Math Library Routines #include <stdio.h> // Header Datei für Standard I/O Routinen #include <stdlib.h> // Header Datei für Standard Library #include <gl\gl.h> // Header Datei für die OpenGL32 Library #include <gl\glu.h> // Header Datei für die GLu32 Library #include <gl\glaux.h> // Header Datei für dieGlaux Library typedef struct point_3d { // Struktur für einen 3-Dimensionalen Punkt ( NEU ) double x, y, z; } POINT_3D; typedef struct bpatch { // Struktur für ein Bezier Patch 3ten Grades ( NEU ) POINT_3D anchors[4][4]; // 4x4 Gitter an Anker-Punkten GLuint dlBPatch; // Display Liste für Bezier Patch GLuint texture; // Textur für das Patch } BEZIER_PATCH; HDC hDC=NULL; // Privater GDI Device Context HGLRC hRC=NULL; // Permanenter Rendering Context HWND hWnd=NULL; // Enthält unser Fenster-Handle HINSTANCE hInstance; // Enthält die Instanz der Applikation DEVMODE DMsaved; // speichert die vorherigen Bildschirmeinstellungen ( NEU ) bool keys[256]; // Array das für die Tastatur Routine verwendet wird bool active=TRUE; // Fenster Aktiv Flag standardmäßig auf TRUE gesetzt bool fullscreen=TRUE; // Fullscreen Flag ist standardmäßig auf TRUE gesetzt GLfloat rotz = 0.0f; // Rotation um die Z-Achse BEZIER_PATCH mybezier; // Das Bezier Patch welches wir verwenden werden ( NEU ) BOOL showCPoints=TRUE; // schaltet das Anzeigen des Kontroll-Punkt-Gitters ( NEU ) int divs = 7; // Anzahl der Intrapolationen(steuert Polygon Auflösung) ( NEU ) LRESULT CALLBACK WndProc(HWND, UINT, WPARAM, LPARAM); // Deklaration für WndProc
Die folgenden Funktionen sind nur ein paar kleine Funktionen für einfache Vektor-Mathematik. Wenn Sie ein Fan von C++ sind, könnten Sie auch eine Punkt-Klasse in betracht ziehen (stellen Sie sicher, dass diese 3D ist).// Addiert 2 Punkte. Benutzen Sie nicht einfach '+' ;) POINT_3D pointAdd(POINT_3D p, POINT_3D q) { p.x += q.x; p.y += q.y; p.z += q.z; return p; } // Multiplziert einen Punkt un eine Konstante. Benutzen Sie nicht einfach '*' POINT_3D pointTimes(double c, POINT_3D p) { p.x *= c; p.y *= c; p.z *= c; return p; } // Funktion zur schnellen Punkt-Erzeugung POINT_3D makePoint(double a, double b, double c) { POINT_3D p; p.x = a; p.y = b; p.z = c; return p; }
Das ist grundlegend nur die Basis-Funktion 3ten Grades in C. Ihr wird eine Variable u und ein Array von 4 Punkten übergeben und berechnet dann einen Punkt auf der Kurve. Indem u in gleichen Schritten zwischn 0 und 1 erhöht wird, erhalten wir eine nette Annäherung der Kurve.// berechnet Polygon dritten Grades basierend auf einem Array aus 4 Punkten // und einer einzelnen Variable (u) welche in der Regel zwischen 0 und 1 ist POINT_3D Bernstein(float u, POINT_3D *p) { POINT_3D a, b, c, d, r; a = pointTimes(pow(u,3), p[0]); b = pointTimes(3*pow(u,2)*(1-u), p[1]); c = pointTimes(3*u*pow((1-u),2), p[2]); d = pointTimes(pow((1-u),3), p[3]); r = pointAdd(pointAdd(a, b), pointAdd(c, d)); return r; }
Diese Funktion macht den Löwenanteil der Arbeit, indem Sie alle Triangle Strips (Dreiecks Streifen) erzeugt und in einer Display Liste speichert. Wir machen das, damit wir den Patch nicht jeden Frame erneut berechnen müssen, sondern nur dann, wenn er sich ändert. Nebenbei, ein cooler Effekt wäre es, wenn Sie versuchen würden das Morphing Tutorial zu verwenden und die Kontrollpunkte des Patch's morphen würden. Das würde einen coolen weichen, organischen Morphing-Effekt ergeben, für realtiv wenig Overhead (da Sie nur 16 Punkte morphen müssen, aber neu berechnen müssten). Das 'last' Array wird benutzt, um die vorherogen Linien an Punkten zu behalten (da ein Triangle Strip beide Reihen benötigt). Außerdem werden die Texturkoordinaten berechnet, indem die Werte u und v als Prozente verwendet werden (planares Mapping).
Was wir nicht machen ist die Berechnung des Normalenvektors für die Beleuchtung. Wenn es dazu kommt haben Sie grundsätzlich zwei Möglichkeiten. Die erste ist, die Mitte jeden Dreiecks zu finden, dann benutzten Sie etwas Matematik und berechnen die Tangente auf der X und Y-Achse, dann bilden Sie das Kreuzprodukt, damit die Vektoren senkrecht zueinander stehen, DANN normalisieren Sie den Vektor und benutzen dies als den Normalenvektor. ODER (ja, es gibt einen schnelleren Weg) Sie schummeln etwas und benutzen einfach den Normalenvektor des Dreiecks (berechnen Sie es, wie Sie es bevorzugen), um eine ziemlich gute Annäherug zu erhalten. Ich bevorzuge letzteres; der Geschwindigkeitsvorteil ist meiner Meinung nach vorzuziehen, da es das klein wenige extra Realismus nicht Wert wäre.// erzeugt eine Display Liste basierend auf den Daten aus dem Patch // und der Anzahl der Divisionen GLuint genBezier(BEZIER_PATCH patch, int divs) { int u = 0, v; float py, px, pyold; GLuint drawlist = glGenLists(1); // erzeuge die Display Liste POINT_3D temp[4]; POINT_3D *last = (POINT_3D*)malloc(sizeof(POINT_3D)*(divs+1)); // Array an Punkten, um die erste Linie Polygone zu kennzeichnen if (patch.dlBPatch != NULL) // werde alle alten Display Listen los glDeleteLists(patch.dlBPatch, 1); temp[0] = patch.anchors[0][3]; // die erste hergeleitete Kurve (entlängs der X-Achse) temp[1] = patch.anchors[1][3]; temp[2] = patch.anchors[2][3]; temp[3] = patch.anchors[3][3]; for (v=0;v// erzeuge die erste Linien an Punkten px = ((float)v)/((float)divs); // Prozent entlängs der Y-Achse // benutze die 4 Punkte aus der hergeleiteten Kurve, um die Punkte entlängs der Kurve zu berechnen last[v] = Bernstein(px, temp); } glNewList(drawlist, GL_COMPILE); // Starte eine neue Display Liste glBindTexture(GL_TEXTURE_2D, patch.texture); // Binde die Texturen for (u=1;u// Prozent entlängs der Y-Achse pyold = ((float)u-1.0f)/((float)divs); // Prozent entlängs der alten Y-Achse temp[0] = Bernstein(py, patch.anchors[0]); // berechne neue Bezier Punkte temp[1] = Bernstein(py, patch.anchors[1]); temp[2] = Bernstein(py, patch.anchors[2]); temp[3] = Bernstein(py, patch.anchors[3]); glBegin(GL_TRIANGLE_STRIP); // Beginne einen neuen Triangle Strip for (v=0;v// Prozent entlängs der X-Achse glTexCoord2f(pyold, px); // wende die alten Texturkoordinaten an glVertex3d(last[v].x, last[v].y, last[v].z); // alter Punkt last[v] = Bernstein(px, temp); // erzeuge neuen Punkt glTexCoord2f(py, px); // wende die neuen Texturkoordinaten an glVertex3d(last[v].x, last[v].y, last[v].z); // Neuer Punkt } glEnd(); // BEENDE Triangle Strip } glEndList(); // BEENDE die Liste free(last); // gebe das alte Vertices-Array frei return drawlist; // gebe die Display Liste zurück }
Hier laden wir lediglich die Matrix mit ein paar Werten, die ich gewählt habe, weil ich denke, dass sie cool aussehen. Spielen Sie einfach damit herum und schauen Sie, was dabei herauskommt. :-)void initBezier(void) { mybezier.anchors[0][0] = makePoint(-0.75, -0.75, -0.50); // Setze die Bezier Vertices mybezier.anchors[0][1] = makePoint(-0.25, -0.75, 0.00); mybezier.anchors[0][2] = makePoint( 0.25, -0.75, 0.00); mybezier.anchors[0][3] = makePoint( 0.75, -0.75, -0.50); mybezier.anchors[1][0] = makePoint(-0.75, -0.25, -0.75); mybezier.anchors[1][1] = makePoint(-0.25, -0.25, 0.50); mybezier.anchors[1][2] = makePoint( 0.25, -0.25, 0.50); mybezier.anchors[1][3] = makePoint( 0.75, -0.25, -0.75); mybezier.anchors[2][0] = makePoint(-0.75, 0.25, 0.00); mybezier.anchors[2][1] = makePoint(-0.25, 0.25, -0.50); mybezier.anchors[2][2] = makePoint( 0.25, 0.25, -0.50); mybezier.anchors[2][3] = makePoint( 0.75, 0.25, 0.00); mybezier.anchors[3][0] = makePoint(-0.75, 0.75, -0.50); mybezier.anchors[3][1] = makePoint(-0.25, 0.75, -1.00); mybezier.anchors[3][2] = makePoint( 0.25, 0.75, -1.00); mybezier.anchors[3][3] = makePoint( 0.75, 0.75, -0.50); mybezier.dlBPatch = NULL; // mache weiter und initialisiere dieses mit NULL }
Dies ist lediglich eine optimierte Routine um ein einzelnen Bitmap zu laden. Sie kann einfach verwendet werden, um ein Array davon zu laden, indem Sie einfach eine einfache Schleife verwenden.// Lade Bitmaps und konvertiere in Texturen BOOL LoadGLTexture(GLuint *texPntr, char* name) { BOOL success = FALSE; AUX_RGBImageRec *TextureImage = NULL; glGenTextures(1, texPntr); // erzeuge 1 Textur FILE* test=NULL; TextureImage = NULL; test = fopen(name, "r"); // Teste, ob die Datei existiert if (test != NULL) { // wenn ja fclose(test); // schließe die Datei TextureImage = auxDIBImageLoad(name); // und lade die Textur } if (TextureImage != NULL) { // wenn sie geladen wurde success = TRUE; // normalerweise benutzt die Textur-Erzeugung Daten aus dem Bitmap glBindTexture(GL_TEXTURE_2D, *texPntr); glTexImage2D(GL_TEXTURE_2D, 0, 3, TextureImage->sizeX, TextureImage->sizeY, 0, GL_RGB, GL_UNSIGNED_BYTE, TextureImage->data); glTexParameteri(GL_TEXTURE_2D,GL_TEXTURE_MIN_FILTER,GL_LINEAR); glTexParameteri(GL_TEXTURE_2D,GL_TEXTURE_MAG_FILTER,GL_LINEAR); } if (TextureImage->data) free(TextureImage->data); return success; }
Fügen Sie die Patch Initialisierung einfach hier ein. Sie würden das immer dann machen, wenn Sie ein Patch erzeugen. Erneut wäre das ein cooler Platz um C++ einzusetzen (Bezier Klasse?).int InitGL(GLvoid) // Der ganze Setup Kram für OpenGL kommt hier rein { glEnable(GL_TEXTURE_2D); // aktiviert Textur Mapping glShadeModel(GL_SMOOTH); // aktiviert Smooth Shading glClearColor(0.05f, 0.05f, 0.05f, 0.5f); // Schwarzer Hintergrund glClearDepth(1.0f); // Depth Buffer Setup glEnable(GL_DEPTH_TEST); // aktiviert Depth Testing glDepthFunc(GL_LEQUAL); // Die Art des auszuführenden Depth Test glHint(GL_PERSPECTIVE_CORRECTION_HINT, GL_NICEST); // wirklich nette Perspektiven Berechnungen initBezier(); // Initialisiert das Bezier Kontroll-Gitter ( NEU ) LoadGLTexture(&(mybezier.texture), "./Data/NeHe.bmp"); // Lade die Textur ( NEU ) mybezier.dlBPatch = genBezier(mybezier, divs); // erzeuge Patch ( NEU ) return TRUE; // Initialisierung war in Ordnung }
Als erstes rufen Sie die Bezier Display Liste auf. Dann (wenn die Umriße angeschaltet sind), zeichne die Linien, die die Kontroll-Punkte verbinden. Sie können diese an und ausschalten, indem Sie die LEERTASTE drücken.int DrawGLScene(GLvoid) { // Hier kommt der ganze Zeichnen-Kram hin int i, j; glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); // Lösche den Bildschirm und den Depth-Buffer glLoadIdentity(); // Resette die aktuelle Modelview Matrix glTranslatef(0.0f,0.0f,-4.0f); // 1.5 Einheiten nach Links dann 6.0 Einheiten in den Bildschirm hinein glRotatef(-75.0f,1.0f,0.0f,0.0f); glRotatef(rotz,0.0f,0.0f,1.0f); // Rotiere das Dreieck auf der Z-Achse glCallList(mybezier.dlBPatch); // rufe die Bezier Display Liste auf // Dies muss nur aktualisiert werden, wenn das Patch geändert wird if (showCPoints) { // wenn das Gitter gezeichnet werden soll glDisable(GL_TEXTURE_2D); glColor3f(1.0f,0.0f,0.0f); for(i=0;i// zeichne die horizontalen Linien glBegin(GL_LINE_STRIP); for(j=0;j// zeichne die vertikalen Linien glBegin(GL_LINE_STRIP); for(j=0;j// weiter geht's }
Diese Funktion enthält etwas modifizierten Code, um Ihre Projekte kompatibler zu halten. Es hat nichts mit Bezier Kurven zu tun, aber behebt ein kleines Problem beim Zurückschalten der Auflösung, nach dem Fullscreen-Modus, der bei einigen Grafikkarten auftritt (inklusiver meiner, einer alten ATI Rage PRO und ein paar anderen). Ich hoffe Sie verwenden das von nun an, so dass ich und andere mit ähnlichen Karten euren coolen GL Beispiel Codes korrekt ansehen kann. Um diese Modiifkation vorzunehmen, ändern Sie die KillGLWindow(), stellen Sie sicher, dass Sie DMsaved defniert haben und ändern Sie die eine Zeile in CreateGlWindow() (ist markiert).GLvoid KillGLWindow(GLvoid) // Entferne das Fenster korrekt { if (fullscreen) // Sind wir im Fullscreen Modus? { if (!ChangeDisplaySettings(NULL,CDS_TEST)) { // wenn der Shortcut nicht funktionier ( NEU ) ChangeDisplaySettings(NULL,CDS_RESET); // mache es trotzdem (um die Werte aus der Registry zu holen) ( NEU ) ChangeDisplaySettings(&DMsaved,CDS_RESET); // ändere sie auf die gespeicherten Einstellungen ( NEU ) } else { ChangeDisplaySettings(NULL,CDS_RESET); // Wenn es funktioniert, mache weiter ( NEU ) } ShowCursor(TRUE); // Zeige den Maus-Zeiger } if (hRC) // Haben wir einen Rendering Context? { if (!wglMakeCurrent(NULL,NULL)) // Können wir den DC und RC Kontext freigeben? { MessageBox(NULL,"Release Of DC And RC Failed.","SHUTDOWN ERROR",MB_OK | MB_ICONINFORMATION); } if (!wglDeleteContext(hRC)) // Können wir den RC löschen? { MessageBox(NULL,"Release Rendering Context Failed.","SHUTDOWN ERROR",MB_OK | MB_ICONINFORMATION); } hRC=NULL; // Setze RC auf NULL } if (hDC && !ReleaseDC(hWnd,hDC)) // Können wir DC freigeben? { MessageBox(NULL,"Release Device Context Failed.","SHUTDOWN ERROR",MB_OK | MB_ICONINFORMATION); hDC=NULL; // Setze DC auf NULL } if (hWnd && !DestroyWindow(hWnd)) // Können wir das Fenster zerstören? { MessageBox(NULL,"Could Not Release hWnd.","SHUTDOWN ERROR",MB_OK | MB_ICONINFORMATION); hWnd=NULL; // Setze hWnd auf NULL } if (!UnregisterClass("OpenGL",hInstance)) // Können wir die Klasse de-registrieren? { MessageBox(NULL,"Could Not Unregister Class.","SHUTDOWN ERROR",MB_OK | MB_ICONINFORMATION); hInstance=NULL; // Setze hInstance auf NULL } }
Der EnumDisplaySettings() Befehl wurde hinzugefügt um die alten Display-Einstellungen zu speichern. (Teile der alten Grafikkartenprobleme wurden behoben).// Dieser Code erzeugt unser OpenGL Fenster. Parameter sind: // title - Titel der im Fenster erscheinen soll // width - Breite des GL Fensters oder Fullscreen Modus // height - Höhe des GL Fensters oder Fullscreen Modus // bits - Anzahl der zu benutzenden Farben (8/16/24/32) // fullscreenflag - Use Fullscreen Mode (TRUE) Or Windowed Mode (FALSE)
BOOL CreateGLWindow(char* title, int width, int height, int bits, bool fullscreenflag)
{
GLuint PixelFormat; // Enthält die Ergebnisse nachdem nach was passendem gesucht wurde
WNDCLASS wc; // Fenster Klassen Struktur
DWORD dwExStyle; // erweiterter Fenster-Stil
DWORD dwStyle; // Fenster-Stil
RECT WindowRect; // Enthält die obere linke / untere rechte Eckwerte des Rechtecks
WindowRect.left=(long)0; // Setze linken Wert auf 0
WindowRect.right=(long)width; // Setze rechten Wert auf die gewünschte Breite
WindowRect.top=(long)0; // Setze den oberen Wert auf 0
WindowRect.bottom=(long)height; // Setze unteren Wert auf die gewünschte Höhe
fullscreen=fullscreenflag; // Setze das globale Fullscreen Flag
hInstance = GetModuleHandle(NULL); // Ermittle die Instanz für unser Fenster
wc.style = CS_HREDRAW | CS_VREDRAW | CS_OWNDC; // Zeichne neu beim bewegen und eigener DC für's Fenster
wc.lpfnWndProc = (WNDPROC) WndProc; // WndProc behandelt die Nachrichten
wc.cbClsExtra = 0; // Keine extra Fenster-Daten
wc.cbWndExtra = 0; // Keine extra Fenster-Daten
wc.hInstance = hInstance; // Setze die Instanz
wc.hIcon = LoadIcon(NULL, IDI_WINLOGO); // Lade das Standard-Icon
wc.hCursor = LoadCursor(NULL, IDC_ARROW); // Lade den Pfeil-Zeiger
wc.hbrBackground = NULL; // es wird kein Hintergrund für GL benötigt
wc.lpszMenuName = NULL; // Wir wollen kein Menü
wc.lpszClassName = "OpenGL"; // Setze den Klassen-Namen
EnumDisplaySettings(NULL, ENUM_CURRENT_SETTINGS, &DMsaved); // speichere den aktuellen Display Status ( NEU )
if (fullscreen) // Fullscreen Modus?
{
DEVMODE dmScreenSettings; // Device Modus
memset(&dmScreenSettings,0,sizeof(dmScreenSettings)); // Stelle sicher, dass der Speicher geleert ist
dmScreenSettings.dmSize=sizeof(dmScreenSettings); // Größe der Devmode Struktur
dmScreenSettings.dmPelsWidth = width; // ausgewählte Screen Breite
dmScreenSettings.dmPelsHeight = height; // ausgewählte Screen Höhe
dmScreenSettings.dmBitsPerPel = bits; // ausgewählte Bits Per Pixel
dmScreenSettings.dmFields=DM_BITSPERPEL|DM_PELSWIDTH|DM_PELSHEIGHT;
... Code Cut To Save Space (No Further Changes To This Function) ...
return TRUE; // Erfolg
}
Alles was ich hier hinzugefügt habe, sind Befehl, um die Fläche zu rotieren, die Auflösung zu erhöhen / runter zu setzen und die Kontrolllinien an und auszuschalten.
int WINAPI WinMain( HINSTANCE hInstance, // Instanz
HINSTANCE hPrevInstance, // vorherige Instanz
LPSTR lpCmdLine, // Kommandozeilen Parameter
int nCmdShow) // Fenster Anzeige Status
{
MSG msg; // Windows Nachrichten Struktur
BOOL done=FALSE; // Bool Variable um die Schleife zu beenden
// Frage den Benutzer, in welchen Modus er starten will
if (MessageBox(NULL,"Would You Like To Run In Fullscreen Mode?", "Start FullScreen?",MB_YESNO|MB_ICONQUESTION)==IDNO)
{
fullscreen=FALSE; // Fenster-Modus
}
// erzeuge unser OpenGL Fenster
if (!CreateGLWindow("NeHe's Solid Object Tutorial",640,480,16,fullscreen))
{
return 0; // Beende, wenn Fenster nicht erzeugt wurde
}
while(!done) // Schleife die so lange läuft, bis done=TRUE
{
if (PeekMessage(&msg,NULL,0,0,PM_REMOVE)) // Wartet eine Nachricht?
{
if (msg.message==WM_QUIT) // Haben wir eine Nachricht zum beenden erhalten?
{
done=TRUE; // Wenn ja done=TRUE
}
else // Wenn nicht, bearbeite die Fenster-Nachrichten
{
TranslateMessage(&msg); // Übersetze die Nachricht
DispatchMessage(&msg); // bearbeite die Nachricht
}
}
else // Wenn da keine Nachrichten sind
{
// Zeichne die Szene. Schaue, ob ESC oder DrawGLScene() zum beenden signalisieren
if ((active && !DrawGLScene()) || keys[VK_ESCAPE]) // Activ? Soll beendet werden?
{
done=TRUE; // ESC oder DrawGLScene Signalisiert, dass Beendet werden soll
}
else // Es ist noch nicht Zeit zum beenden, zeichne Screen neu
{
SwapBuffers(hDC); // Swap Buffers (Double Buffering)
}
if (keys[VK_LEFT]) rotz -= 0.8f; // rotiere links ( NEU )
if (keys[VK_RIGHT]) rotz += 0.8f; // rotiere rechts ( NEU )
if (keys[VK_UP]) { // mehr Details ( NEU )
divs++;
mybezier.dlBPatch = genBezier(mybezier, divs); // akutalisiere die Fläche
keys[VK_UP] = FALSE;
}
if (keys[VK_DOWN] && divs > 1) { // weniger Details ( NEU )
divs--;
mybezier.dlBPatch = genBezier(mybezier, divs); // aktualisiere die Fläche
keys[VK_DOWN] = FALSE;
}
if (keys[VK_SPACE]) { // LEERTASTE invertiert showCPoints ( NEU )
showCPoints = !showCPoints;
keys[VK_SPACE] = FALSE;
}
if (keys[VK_F1]) // Wurde F1 gedrückt?
{
keys[VK_F1]=FALSE; // Wenn ja, setze Taste auf FALSE
KillGLWindow(); // Kill unser aktuelles Fenster
fullscreen=!fullscreen; // Wechsel zwischen Fullscreen und Fester-Modus
// Erzeuge unser OpenGL Fenster erneut
if (!CreateGLWindow("NeHe's Solid Object Tutorial",640,480,16,fullscreen))
{
return 0; // Beenden, wenn das Fenster nicht erzeugt wurde
}
}
}
}
// Shutdown
KillGLWindow(); // Kill das Fenster
return (msg.wParam); // Beende das Programm
}
Nun, ich hoffe dieses Tutorial hat etwas Licht in die Sache gebracht und Sie lieben nun Bezier Kurven genauso sehr, wie ich ;-). Wenn Sie dieses Tutorial mögen, werde ich vielleicht ein weiteres Tutorial über NURBS Kurven schreiben, wenn Interesse besteht. Mailen Sie mir und lassen Sie mich wissen, was Sie über dieses Tutorial denken.
Über den Autor: David Nikdel ist zur Zeit 18 und Senior an der Bartow Senior High School. Seine aktuellen Projekte beinhalten ein Research Paper über gekrümmte Flächen in 3D Grpahiken, ein OpenGL basiertes Spiel namens Blazing Sands und faulenzen. Seine Hobbies sind programmieren, Fussball und Paintball. Er wird (hoffentlich) nächstes Jahr an der Georgia Tech anfangen.
David Nikdel
Jeff Molofee (NeHe)
* DOWNLOAD Visual C++ Code für diese Lektion.
* DOWNLOAD Borland C++ Builder 6 Code für diese Lektion. ( Conversion by Christian Kindahl )
* DOWNLOAD Code Warrior 5.3 Code für diese Lektion. ( Conversion by Scott Lupton )
* DOWNLOAD Delphi Code für diese Lektion. ( Conversion by Joachim Rohde )
* DOWNLOAD Dev C++ Code für diese Lektion. ( Conversion by Dan )
* DOWNLOAD Euphoria Code für diese Lektion. ( Conversion by Evan Marshall )
* DOWNLOAD LCC Win32 Code für diese Lektion. ( Conversion by Robert Wishlaw )
* DOWNLOAD Linux/GLX Code für diese Lektion. ( Conversion by Rodolphe Suescun )
* DOWNLOAD LWJGL Code für diese Lektion. ( Conversion by Mark Bernard )
* DOWNLOAD Mac OS X/Cocoa Code für diese Lektion. ( Conversion by Bryan Blackburn )
* DOWNLOAD Visual Studio .NET Code für diese Lektion. ( Conversion by Grant James )
Deutsche Übersetzung: Joachim Rohde
Der original Text ist hier zu finden.
Die original OpenGL Tutorials stammen von NeHe's Seite.