Lektion 44
Hallo, ich bin's wieder mit einem neuen Tutorial. In diesem werde ich Ihnen zeigen, wie Lens-Flares mit der erweiterten glCamera Klasse gemacht werden. Wenn Sie eine Lens Flare betrachten, werden Sie feststellen, dass sie alles eins gemeinsam haben. Alle scheinen durch die Mitte des Screens zu bewegen. Wenn Sie das wissen, können sie die Z-Koordinate einfach weglassen und Ihre Flares alle 2D machen. Das einzige Problem dabei ist, wie finden Sie ohne Z-Achse heraus, ob Ihre Kamera auf die Lichtquelle zeigt oder nicht? In diesem Tutorial machen wir 3D Lens Flares, bereiten Sie sich also auf ein wenig Mathematik vor. Wir müssen einige Dinge der Kamera-Klasse hinzufügen, um das zu realisieren. Als erstes brauchen wir ein paar Funktionen, die ermitteln, ob ein Punkt oder Sphere im aktuellen Sichtbereich der Kamera liegt. Dann brauchen wir ein paar Texturen, die wir für die Flares benötigen und letztendlich brauch wir all das, ohne unseren Prozessor zu killen!
Ich muss es leider zugeben, aber da war ein Bug in der letzten Kamera-Klasse, der gefixt werden muss. Bevor wir anfangen, ist hier also der Code, der den Bug fixt. Die Funktion SetPerspective muss wie folgt geändert werden.
void glCamera::SetPrespective()
{
GLfloat Matrix[16];
glVector v;
// benutze glRotate um unseren Richtungsvektor zu berechnen
glRotatef(m_HeadingDegrees, 0.0f, 1.0f, 0.0f);
glRotatef(m_PitchDegrees, 1.0f, 0.0f, 0.0f);
// hole die resultierende Matrix von OpenGL, sie wird unseren
// Richtungsvektor in der 3ten Reihe haben
glGetFloatv(GL_MODELVIEW_MATRIX, Matrix);
// hole den Richtungsvektor aus der Matrix. Element 10 muss invertiert werden!
m_DirectionVector.i = Matrix[8];
m_DirectionVector.j = Matrix[9];
m_DirectionVector.k = -Matrix[10];
// Ok lösche die Ergebnisse aus der letzten Berechnung
glLoadIdentity();
// Rotiere die Szene, um die richtige Orientierung zu erhalten
glRotatef(m_PitchDegrees, 1.0f, 0.0f, 0.0f);
glRotatef(m_HeadingDegrees, 0.0f, 1.0f, 0.0f);
// skaliere die Richtung anhand unserer Geschwindigkeit.
v = m_DirectionVector;
v *= m_ForwardVelocity;
// Inkrementiere unsere Position um den Vektor
m_Position.x += v.i;
m_Position.y += v.j;
m_Position.z += v.k;
// translatiere zu unserer neuen Position.
glTranslatef(-m_Position.x, -m_Position.y, -m_Position.z);
}
Ok, nun können wir anfangen. Wir werden 4 seperate Texturen benutzen, um unsere Lens Falre zu erzeugen. Die erste Textur die wir brauchen nenne ich 'Big Glow' (großes Glühen) Textur. Unsere Lichtquelle wird von einem nebligen Glühen eingehüllt. Diese Textur wird immer an der Lichtquelle positioniert. Die nächste Textur ist die Streaks (Streifen) Textur. Diese Textur umhüllt unsere Lichtquelle mit Streifen. Diese Textur wird ebenso an der Lichtquelle positioniert. Die Glow Textur (nicht Big Glow) wird dynamisch über den Screen bewegt. Die Glow Textur ist ähnlich der Big Glow Textur, aber ich habe festgestellt, dass eine kleinere Textur hier besser aussieht, als einfach nur Big Glow. Und letztlich brauch wir eine Halo (Heiligenschein) Textur. Das sind die leer aussehende Ringe für die Flare und werden dynamisch über den Bildschirm, abhängig von der Kamera Orientierung und Position, bewegt. Es gibt noch ein paar andere Arten an Texturen, die Sie für Lens Flares benutzen können, wenn Sie wollen. Das liegt an Ihnen. Schauen Sie sich die Ressourcen am Ende des Tutorials für weitere Informationen an. Es folgen einige Beispiele dieser Texturen.
großes Glühen

|
|
Streifen

|
Glühen

|
|
'Heiligenschein'

|
Nun, da Sie eine Vorstellung haben, was wir zeichnen werden, sprechen wir darüber, wann wir die Lens Flares zeichnen müssen. Es ist offensichtlich, dass wir die Lens Flares nicht zeichnen wollen, wenn wir nicht die Lichtquelle anschauen, deshalb brauchen wir einen Weg, den Sichtbereich oder das Frustrum von OpenGL zu ermitteln. Wir könnten das machen, indem wir die Modelview und die Projektions Matrix kombinieren und dann die Clipping Ebenen herausfinden, die OpenGL benutzt. Ein anderer Weg herauszufinden, ob ein Punkt im Sichtbereich liegt, wäre die Benutzung von Extensions. Wir könnten die GL_HP_occlusion_test oder GL_NV_occlusion_query Extensions verwenden, um herauszufinden, ob ein Vertex im Sichtbereich der Kamera liegt, da aber nicht jeder diese Extensionen hat, beschränken wir uns auf den altbewährten Weg in diesem Tutorial. Es folgt die UpdateFrustrum Funktion.
void glCamera::UpdateFrustum()
{
GLfloat clip[16];
GLfloat proj[16];
GLfloat modl[16];
GLfloat t;
// ermittle die aktuelle PROJEKTIONS Matrix von OpenGL
glGetFloatv( GL_PROJECTION_MATRIX, proj );
// ermittle die aktuelle MODELVIEW Matrix von OpenGL
glGetFloatv( GL_MODELVIEW_MATRIX, modl );
// kombiniere die beiden Matrizen (multipliziere Projektion mit Modelview)
clip[ 0] = modl[ 0] * proj[ 0] + modl[ 1] * proj[ 4] + modl[ 2] * proj[ 8] + modl[ 3] * proj[12];
clip[ 1] = modl[ 0] * proj[ 1] + modl[ 1] * proj[ 5] + modl[ 2] * proj[ 9] + modl[ 3] * proj[13];
clip[ 2] = modl[ 0] * proj[ 2] + modl[ 1] * proj[ 6] + modl[ 2] * proj[10] + modl[ 3] * proj[14];
clip[ 3] = modl[ 0] * proj[ 3] + modl[ 1] * proj[ 7] + modl[ 2] * proj[11] + modl[ 3] * proj[15];
clip[ 4] = modl[ 4] * proj[ 0] + modl[ 5] * proj[ 4] + modl[ 6] * proj[ 8] + modl[ 7] * proj[12];
clip[ 5] = modl[ 4] * proj[ 1] + modl[ 5] * proj[ 5] + modl[ 6] * proj[ 9] + modl[ 7] * proj[13];
clip[ 6] = modl[ 4] * proj[ 2] + modl[ 5] * proj[ 6] + modl[ 6] * proj[10] + modl[ 7] * proj[14];
clip[ 7] = modl[ 4] * proj[ 3] + modl[ 5] * proj[ 7] + modl[ 6] * proj[11] + modl[ 7] * proj[15];
clip[ 8] = modl[ 8] * proj[ 0] + modl[ 9] * proj[ 4] + modl[10] * proj[ 8] + modl[11] * proj[12];
clip[ 9] = modl[ 8] * proj[ 1] + modl[ 9] * proj[ 5] + modl[10] * proj[ 9] + modl[11] * proj[13];
clip[10] = modl[ 8] * proj[ 2] + modl[ 9] * proj[ 6] + modl[10] * proj[10] + modl[11] * proj[14];
clip[11] = modl[ 8] * proj[ 3] + modl[ 9] * proj[ 7] + modl[10] * proj[11] + modl[11] * proj[15];
clip[12] = modl[12] * proj[ 0] + modl[13] * proj[ 4] + modl[14] * proj[ 8] + modl[15] * proj[12];
clip[13] = modl[12] * proj[ 1] + modl[13] * proj[ 5] + modl[14] * proj[ 9] + modl[15] * proj[13];
clip[14] = modl[12] * proj[ 2] + modl[13] * proj[ 6] + modl[14] * proj[10] + modl[15] * proj[14];
clip[15] = modl[12] * proj[ 3] + modl[13] * proj[ 7] + modl[14] * proj[11] + modl[15] * proj[15];
// extrahiere die Zahlen für die RECHTE Ebene
m_Frustum[0][0] = clip[ 3] - clip[ 0];
m_Frustum[0][1] = clip[ 7] - clip[ 4];
m_Frustum[0][2] = clip[11] - clip[ 8];
m_Frustum[0][3] = clip[15] - clip[12];
// Normalisiere das Ergebniss
t = GLfloat(sqrt( m_Frustum[0][0] * m_Frustum[0][0] + m_Frustum[0][1] * m_Frustum[0][1] + m_Frustum[0][2] * m_Frustum[0][2] ));
m_Frustum[0][0] /= t;
m_Frustum[0][1] /= t;
m_Frustum[0][2] /= t;
m_Frustum[0][3] /= t;
// extrahiere die Zahlen für die LINKE Ebene
m_Frustum[1][0] = clip[ 3] + clip[ 0];
m_Frustum[1][1] = clip[ 7] + clip[ 4];
m_Frustum[1][2] = clip[11] + clip[ 8];
m_Frustum[1][3] = clip[15] + clip[12];
// Normalisiere das Ergebniss
t = GLfloat(sqrt( m_Frustum[1][0] * m_Frustum[1][0] + m_Frustum[1][1] * m_Frustum[1][1] + m_Frustum[1][2] * m_Frustum[1][2] ));
m_Frustum[1][0] /= t;
m_Frustum[1][1] /= t;
m_Frustum[1][2] /= t;
m_Frustum[1][3] /= t;
// extrahiere die Zahlen für die UNTERE Ebene
m_Frustum[2][0] = clip[ 3] + clip[ 1];
m_Frustum[2][1] = clip[ 7] + clip[ 5];
m_Frustum[2][2] = clip[11] + clip[ 9];
m_Frustum[2][3] = clip[15] + clip[13];
// Normalisiere das Ergebniss
t = GLfloat(sqrt( m_Frustum[2][0] * m_Frustum[2][0] + m_Frustum[2][1] * m_Frustum[2][1] + m_Frustum[2][2] * m_Frustum[2][2] ));
m_Frustum[2][0] /= t;
m_Frustum[2][1] /= t;
m_Frustum[2][2] /= t;
m_Frustum[2][3] /= t;
// extrahiere die Zahlen für die OBERE Ebene
m_Frustum[3][0] = clip[ 3] - clip[ 1];
m_Frustum[3][1] = clip[ 7] - clip[ 5];
m_Frustum[3][2] = clip[11] - clip[ 9];
m_Frustum[3][3] = clip[15] - clip[13];
// Normalisiere das Ergebniss
t = GLfloat(sqrt( m_Frustum[3][0] * m_Frustum[3][0] + m_Frustum[3][1] * m_Frustum[3][1] + m_Frustum[3][2] * m_Frustum[3][2] ));
m_Frustum[3][0] /= t;
m_Frustum[3][1] /= t;
m_Frustum[3][2] /= t;
m_Frustum[3][3] /= t;
// extrahiere die Zahlen für die ENTFERNTE Ebene
m_Frustum[4][0] = clip[ 3] - clip[ 2];
m_Frustum[4][1] = clip[ 7] - clip[ 6];
m_Frustum[4][2] = clip[11] - clip[10];
m_Frustum[4][3] = clip[15] - clip[14];
// Normalisiere das Ergebniss
t = GLfloat(sqrt( m_Frustum[4][0] * m_Frustum[4][0] + m_Frustum[4][1] * m_Frustum[4][1] + m_Frustum[4][2] * m_Frustum[4][2] ));
m_Frustum[4][0] /= t;
m_Frustum[4][1] /= t;
m_Frustum[4][2] /= t;
m_Frustum[4][3] /= t;
// extrahiere die Zahlen für die NAHE Ebene
m_Frustum[5][0] = clip[ 3] + clip[ 2];
m_Frustum[5][1] = clip[ 7] + clip[ 6];
m_Frustum[5][2] = clip[11] + clip[10];
m_Frustum[5][3] = clip[15] + clip[14];
// Normalisiere das Ergebniss
t = GLfloat(sqrt( m_Frustum[5][0] * m_Frustum[5][0] + m_Frustum[5][1] * m_Frustum[5][1] + m_Frustum[5][2] * m_Frustum[5][2] ));
m_Frustum[5][0] /= t;
m_Frustum[5][1] /= t;
m_Frustum[5][2] /= t;
m_Frustum[5][3] /= t;
}
Diese Funktion ist ein Monster! Ich bin mir sicher, dass Sie nun wissen, warum es Extensions gibt, die solche Sachen übernehmen. Obwohl die Mathematik dahinter ziemlich einfach ist, ist es die Länge, die es so ätzend macht. In der Funktion eben gibt es 190 Operationen (Multiplikationen, Additionen, Subtraktionen, Divisionen) plus 6 Wurzeln. Da wir diese Funktion jedes Mal aufrufen werden, wenn die Szene gezeichnet wird, wird es die Mühe wert sein, sie zu optimieren. Es folgt eine optimierte Version der Funktion. So lange wir keine Roatation oder Translation and der Projektions Matrix vornehmen, wird die folgende Funktion funktionieren, um die Clipping Ebenen für den Sichtbereich / Frustrum zu ermitteln.
void glCamera::UpdateFrustumFaster()
{
GLfloat clip[16];
GLfloat proj[16];
GLfloat modl[16];
GLfloat t;
// ermittle die aktuelle PROJEKTIONS Matrix von OpenGL
glGetFloatv( GL_PROJECTION_MATRIX, proj );
// ermittle die aktuelle MODELVIEW Matrix von OpenGL
glGetFloatv( GL_MODELVIEW_MATRIX, modl );
// kombiniere die beiden Matrizen (multipliziere Projektion mit Modelview)
// aber behalten Sie im Hinterkopf, dass diese Funktion nur dann funktioniert, wenn Sie Ihre
// Projektions Matrix NICHT rotieren oder translatieren
clip[ 0] = modl[ 0] * proj[ 0];
clip[ 1] = modl[ 1] * proj[ 5];
clip[ 2] = modl[ 2] * proj[10] + modl[ 3] * proj[14];
clip[ 3] = modl[ 2] * proj[11];
clip[ 4] = modl[ 4] * proj[ 0];
clip[ 5] = modl[ 5] * proj[ 5];
clip[ 6] = modl[ 6] * proj[10] + modl[ 7] * proj[14];
clip[ 7] = modl[ 6] * proj[11];
clip[ 8] = modl[ 8] * proj[ 0];
clip[ 9] = modl[ 9] * proj[ 5];
clip[10] = modl[10] * proj[10] + modl[11] * proj[14];
clip[11] = modl[10] * proj[11];
clip[12] = modl[12] * proj[ 0];
clip[13] = modl[13] * proj[ 5];
clip[14] = modl[14] * proj[10] + modl[15] * proj[14];
clip[15] = modl[14] * proj[11];
// extrahiere die Zahlen für die RECHTE Ebene
m_Frustum[0][0] = clip[ 3] - clip[ 0];
m_Frustum[0][1] = clip[ 7] - clip[ 4];
m_Frustum[0][2] = clip[11] - clip[ 8];
m_Frustum[0][3] = clip[15] - clip[12];
// Normalisiere das Ergebniss
t = GLfloat(sqrt( m_Frustum[0][0] * m_Frustum[0][0] + m_Frustum[0][1] * m_Frustum[0][1] + m_Frustum[0][2] * m_Frustum[0][2] ));
m_Frustum[0][0] /= t;
m_Frustum[0][1] /= t;
m_Frustum[0][2] /= t;
m_Frustum[0][3] /= t;
// extrahiere die Zahlen für die LINKE Ebene
m_Frustum[1][0] = clip[ 3] + clip[ 0];
m_Frustum[1][1] = clip[ 7] + clip[ 4];
m_Frustum[1][2] = clip[11] + clip[ 8];
m_Frustum[1][3] = clip[15] + clip[12];
// Normalisiere das Ergebniss
t = GLfloat(sqrt( m_Frustum[1][0] * m_Frustum[1][0] + m_Frustum[1][1] * m_Frustum[1][1] + m_Frustum[1][2] * m_Frustum[1][2] ));
m_Frustum[1][0] /= t;
m_Frustum[1][1] /= t;
m_Frustum[1][2] /= t;
m_Frustum[1][3] /= t;
// extrahiere die Zahlen für die UNTERE Ebene
m_Frustum[2][0] = clip[ 3] + clip[ 1];
m_Frustum[2][1] = clip[ 7] + clip[ 5];
m_Frustum[2][2] = clip[11] + clip[ 9];
m_Frustum[2][3] = clip[15] + clip[13];
// Normalisiere das Ergebniss
t = GLfloat(sqrt( m_Frustum[2][0] * m_Frustum[2][0] + m_Frustum[2][1] * m_Frustum[2][1] + m_Frustum[2][2] * m_Frustum[2][2] ));
m_Frustum[2][0] /= t;
m_Frustum[2][1] /= t;
m_Frustum[2][2] /= t;
m_Frustum[2][3] /= t;
// extrahiere die Zahlen für die OBERE Ebene
m_Frustum[3][0] = clip[ 3] - clip[ 1];
m_Frustum[3][1] = clip[ 7] - clip[ 5];
m_Frustum[3][2] = clip[11] - clip[ 9];
m_Frustum[3][3] = clip[15] - clip[13];
// Normalisiere das Ergebniss
t = GLfloat(sqrt( m_Frustum[3][0] * m_Frustum[3][0] + m_Frustum[3][1] * m_Frustum[3][1] + m_Frustum[3][2] * m_Frustum[3][2] ));
m_Frustum[3][0] /= t;
m_Frustum[3][1] /= t;
m_Frustum[3][2] /= t;
m_Frustum[3][3] /= t;
// extrahiere die Zahlen für die ENTFERNTE Ebene
m_Frustum[4][0] = clip[ 3] - clip[ 2];
m_Frustum[4][1] = clip[ 7] - clip[ 6];
m_Frustum[4][2] = clip[11] - clip[10];
m_Frustum[4][3] = clip[15] - clip[14];
// Normalisiere das Ergebniss
t = GLfloat(sqrt( m_Frustum[4][0] * m_Frustum[4][0] + m_Frustum[4][1] * m_Frustum[4][1] + m_Frustum[4][2] * m_Frustum[4][2] ));
m_Frustum[4][0] /= t;
m_Frustum[4][1] /= t;
m_Frustum[4][2] /= t;
m_Frustum[4][3] /= t;
// extrahiere die Zahlen für die NAHE Ebene
m_Frustum[5][0] = clip[ 3] + clip[ 2];
m_Frustum[5][1] = clip[ 7] + clip[ 6];
m_Frustum[5][2] = clip[11] + clip[10];
m_Frustum[5][3] = clip[15] + clip[14];
// Normalisiere das Ergebniss
t = GLfloat(sqrt( m_Frustum[5][0] * m_Frustum[5][0] + m_Frustum[5][1] * m_Frustum[5][1] + m_Frustum[5][2] * m_Frustum[5][2] ));
m_Frustum[5][0] /= t;
m_Frustum[5][1] /= t;
m_Frustum[5][2] /= t;
m_Frustum[5][3] /= t;
}
Es ist immer noch monströs, aber diese Funktion hat ungefähr nur noch die Hälfte an Operationen als die erste Funktion (102). Die Optimierung ist eine recht einfach. Ich habe einfach alle Multiplikationen rausgenommen, die normalerweise null ergeben, wenn Projektions und Modelview Matrix kombiniert werden. Wenn Sie diese Funktion wirklich optimieren wollen, benutzen Sie statt dessen Extensions. Die Extension macht genau das selbe, aber macht es wesentlich schneller, da die Berechnungen von der Grafik-Hardware durchgeführt werden. Wie dem auch sei, das Aufrufen einer der UpdateFrustrum Funktionen gibt uns ein paar Performance Einbußen, aber wir erreichen einen netten Vorteil dadurch. Wir können nun sagen, ob die Kamera ein Objekt oder Punkt sehen kann. Wenn Sie mehrere verschiedene Objekte in Ihrer Szene haben, profitieren Sie davon, nur diese zu zeichnen, die gerade im Sichtfeld sind. Das ist nützlich wenn Sie viel Terrain zum zeichnen haben und Sie so nicht OpenGL überfordern, indem Sie jeden einzelnen Vertex senden. Es folgt eine Funktion die überprüft, ob ein Punkt im Sichtbereich liegt. Es gibt auch eine SphereInFrustum Funktion in der Klasse, aber ich werde Sie hier nicht aufführen, da beide Funktionen fast identisch sind.
BOOL glCamera::PointInFrustum(glPoint p)
{
int i;
// Die Idee hinter diesem Algorithmus ist, dass wenn der Punkt
// innerhalb der 6 Clipping Ebenen ist, dann ist er innerhalb unseres
// Sichtbereiches, so dass wir True zurückgeben können.
for(i = 0; i <6; i++)
{
if(m_Frustum[i][0] * p.x + m_Frustum[i][1] * p.y + m_Frustum[i][2] * p.z + m_Frustum[i][3]
Nun fordern wir OGL auf, etwas Geometrie für uns zu projizieren, indem die gluProjekt Funktion verwendet wird. Wir forden praktisch von OGL zu raten, wo ein Punkt im Raum in unseren aktuellen Viewport projiziert wird, indem wir den eigentlichen Viewport verwenden und die Transfromation Matrizen unserer Funktion übergeben. Wenn wir der Funktion die aktuellen Matrizen übergeben (die wir mittels der glGet Funktionen erhalten), werden wir die reele Position auf dem Screen erhalten, wo der Punkt gezeichnet wird. Der interessante Teil ist, dass wir ebenso den Z Wert zurückgeliefert bekommen, was bedeuetet, dass wenn wir den WIRKLICHEN Buffer Z Werte auslesen, wir bestimmen können, ob die Flare sichtbar ist oder von Objekten verdeckt wird.
// ########## NEUER CODE von rIO.Spinning Kids ##########
bool glCamera::IsOccluded(glPoint p)
{
GLint viewport[4]; // Platz für Viewport Daten
GLdouble mvmatrix[16], projmatrix[16]; // Platz für Transformatopns Matrix
GLdouble winx, winy, winz; // Platz für zurückgegebene Projektions Koordinaten
GLdouble flareZ; // Hier werden wir das transformierte Flare Z speichern
GLfloat bufferZ; // Hier werden wir das aus dem Buffer ausgelesene Z speichern
glGetIntegerv (GL_VIEWPORT, viewport); // ermittle den aktuellen Viewport
glGetDoublev (GL_MODELVIEW_MATRIX, mvmatrix); // ermittle die aktuelle Model View Matrix
glGetDoublev (GL_PROJECTION_MATRIX, projmatrix); // ermittle die aktuelle Projektions Matrix
// Dies fordert OGL auf, die 2D Position eines 3D Punktes im Viewport zu erraten
gluProject(p.x, p.y, p.z, mvmatrix, projmatrix, viewport, &winx, &winy, &winz);
flareZ = winz;
// Wir lesen einen Pixel aus dem Depth Buffer aus (genau da, wo unser Flare gezeichnet werden soll
glReadPixels(winx, winy,1,1,GL_DEPTH_COMPONENT, GL_FLOAT, &bufferZ);
// Wenn das Buffer Z kleiner als unser geratenes Flare Z ist, dann zeichne nicht
// Das bedeutet, dass etwas vor unserer Flare ist
if (bufferZ < flareZ)
return true;
else
return false;
}
Nun müssen wir uns einem anderen Problem widmen, welches wir haben werden. Da wir 3D Lens Flares erzeugen, wenn wir unsere Flares auf Textur gemappte Quads zeichnen, werden diese vielleicht nicht immer zur Kamera zeigen. Das ist ziemlich schlecht, da unsere Flares ziemlich flach erscheinen können, wenn wir von der Seite aus auf die Lichtquelle schauen. Statt texturierte Quads zu benutzen, könnten wir Punkt Sprites (Point Sprites) verwenden. Point Sprites sind ganz nett, da wir nur einen einzelnen Punkt an OpenGL senden müssen, statt vier Punkten mit Textur-Koordinaten und Sie müssen keine Textur-Koordinaten spezifizieren. Point Sprites sind großartig für Partikel Engines und ebenso für Lens Flares. Da wir uns nur um einen Punkt künmmern müssen, ist das einzige was wir machen müssen, herauszufinden, wo wir die Punkte zeichnen müssen und den entsprechenden Zeichnen-Code aufrufen. Der Nachteil von Point Sprites ist, dass diese zur Zeit nur als Extension (GL_NV_point_sprite) implementiert sind. Um dieses Tutorial für jeden nachvollziehbar zu halten, werde ich erneut Extensionen hier vermeiden. Ein Weg um sicher zu sein, dass unsere Flares immer zur Kamera gerichtet sind, ist einfach die Rotationen umzudrehen, die wir benutzt haben, als wir unsere Perspektive gesetzt haben. Das funktioniert ganz gut, bloss dann nicht mehr, wenn die Kamera jemals hinter die Lichtquelle kommt. Um das zu verhindern, sagen wir, dass es der Kamera niemals erlaubt ist, hinter die Lichtquelle zu kommen, indem wir die Lichtquelle kontinuierlich bewegen, wenn wir die Kamera bewegen. Das gibt uns einen weiteren Nebeneffekt, nämlich, dass die Lichtquelle unendlich weit weg erscheint und es auch den Flares erlaubt ein wenig zu justieren, wenn man sich auf einer Linie bewegt. Genug geredet, es folgt der Code um die nötigen Vektoren und Punkte zu ermitteln.
GLfloat Length = 0.0f;
// Zeichne die Flare nur, wenn wir auf die Lichtquelle schauen
if(SphereInFrustum(m_LightSourcePos, 1.0f) == TRUE)
{
vLightSourceToCamera = m_Position - m_LightSourcePos; // Nun berechne den Vektor der auf die Kamera
// von der Lichtquelle zeigt.
Length = vLightSourceToCamera.Magnitude(); // Speichere die Länge, wir werden sie gleich benötigen
ptIntersect = m_DirectionVector * Length; // Nun suchen wir einen Punkt entlängs des Kamera Richtungsvektor,
// den wir als Schnittpunkt benutzen können.
// Nun translatieren wir diesen Vektor die selbe Distanz herunter
// wie die Kamera. Weg von der Lichtquelle.
ptIntersect += m_Position;
vLightSourceToIntersect = ptIntersect - m_LightSourcePos; // Nun berechnen wir den Vektor, der auf den Schnittpunkt
// von der Lichtquelle zeigt
Length = vLightSourceToIntersect.Magnitude(); // speichere die Länge, wir werden Sie später noch benötigen
vLightSourceToIntersect.Normalize(); // Normalisiere den Vektor, so dass er eine Längeneinheit hat
Als erstes müssen wir den Abstand zwischen Lichtquelle (Light Source Position) und Kamera (Camera Position) herausfinden. Als nächstes benötigen wir einen Schnittpunkt (Intersection Point) mit dem Kamera Richtungsvektor (Camera Direction Vector). Der Abstand zwischen Schnittpunkt und Kamera muss der selbe sein, wie von Lichtquelle zu Kamera. Nun, da wir einen Schnittpunkt haben, können wir einen Vektor finden, mit dem wir die Lens Flares zeichnen können. Folgendes Bild zur Verdeutlichung.
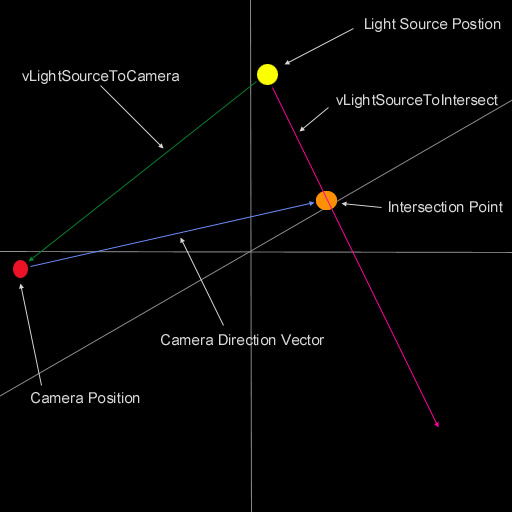
Nun, da wir einen Richtungsvektor haben, um die Lens Flares zu zeichnen, müssen wir nur die Halos und Glows zeichnen. Folgender Cide zeichnet die Flares entlängs des Vektors. Wir erzeugen einen neuen Punkt, indem wir uns X Einheiten entlängs des vLightSourceToIntersect Vektors bewegen und dann das zu Lichtquellen Position addieren.
glEnable(GL_BLEND);
glBlendFunc(GL_SRC_ALPHA, GL_ONE);
glDisable(GL_DEPTH_TEST);
glEnable(GL_TEXTURE_2D);
// ########## NEUER CODE von rIO.Spinning Kids ##########
if (!IsOccluded(m_LightSourcePos)) // überprüfe, ob der Mittelpunkt der Flare verdeckt ist
{
// Rendere den großen nebligen Glow
RenderBigGlow(0.60f, 0.60f, 0.8f, 1.0f, m_LightSourcePos, 16.0f);
// Rendere Streaks
RenderStreaks(0.60f, 0.60f, 0.8f, 1.0f, m_LightSourcePos, 16.0f);
// Rendere den kleinen Glow
RenderGlow(0.8f, 0.8f, 1.0f, 0.5f, m_LightSourcePos, 3.5f);
pt = vLightSourceToIntersect * (Length * 0.1f); // Nun berechne einen Punkt, der 20 %
pt += m_LightSourcePos; // von der Lichtquelle weg ist,
// in Richtung des Schnittpunktes
RenderGlow(0.9f, 0.6f, 0.4f, 0.5f, pt, 0.6f); // Rendere den kleinen Glow
pt = vLightSourceToIntersect * (Length * 0.15f); // Nun berechne einen Punkt der 30 %
pt += m_LightSourcePos; // von der Lichtquelle weg ist,
// in Richtung des Schnittpunktes
RenderHalo(0.8f, 0.5f, 0.6f, 0.5f, pt, 1.7f); // Rendere Halo
pt = vLightSourceToIntersect * (Length * 0.175f); // Nun berechne einen Punkt der 35 %
pt += m_LightSourcePos; // von der Lichtquelle weg ist,
// in Richtung des Schnittpunktes
RenderHalo(0.9f, 0.2f, 0.1f, 0.5f, pt, 0.83f); // Rendere Halo
pt = vLightSourceToIntersect * (Length * 0.285f); // Nun berechne einen Punkt der 57 %
pt += m_LightSourcePos; // von der Lichtquelle weg ist,
// in Richtung des Schnittpunktes
RenderHalo(0.7f, 0.7f, 0.4f, 0.5f, pt, 1.6f); // Rendere Halo
pt = vLightSourceToIntersect * (Length * 0.2755f); // Nun berechne einen Punkt der 55.1 %
pt += m_LightSourcePos; // von der Lichtquelle weg ist,
// in Richtung des Schnittpunktes
RenderGlow(0.9f, 0.9f, 0.2f, 0.5f, pt, 0.8f); // Rendere den kleinen Glow
pt = vLightSourceToIntersect * (Length * 0.4775f); // Nun berechne einen Punkt der 95.5 %
pt += m_LightSourcePos; // von der Lichtquelle weg ist,
// in Richtung des Schnittpunktes
RenderGlow(0.93f, 0.82f, 0.73f, 0.5f, pt, 1.0f); // Rendere den kleinen Glow
pt = vLightSourceToIntersect * (Length * 0.49f); // Nun berechne einen Punkt der 98 %
pt += m_LightSourcePos; // von der Lichtquelle weg ist,
// in Richtung des Schnittpunktes
RenderHalo(0.7f, 0.6f, 0.5f, 0.5f, pt, 1.4f); // Rendere Halo
pt = vLightSourceToIntersect * (Length * 0.65f); // Nun berechne einen Punkt der 130 %
pt += m_LightSourcePos; // von der Lichtquelle weg ist,
// in Richtung des Schnittpunktes
RenderGlow(0.7f, 0.8f, 0.3f, 0.5f, pt, 1.8f); // Rendere den kleinen Glow
pt = vLightSourceToIntersect * (Length * 0.63f); // Nun berechne einen Punkt der 126 %
pt += m_LightSourcePos; // von der Lichtquelle weg ist,
// in Richtung des Schnittpunktes
RenderGlow(0.4f, 0.3f, 0.2f, 0.5f, pt, 1.4f); // Rendere den kleinen Glow
pt = vLightSourceToIntersect * (Length * 0.8f); // Nun berechne einen Punkt der 160 %
pt += m_LightSourcePos; // von der Lichtquelle weg ist,
// in Richtung des Schnittpunktes
RenderHalo(0.7f, 0.5f, 0.5f, 0.5f, pt, 1.4f); // Rendere Halo
pt = vLightSourceToIntersect * (Length * 0.7825f); // Nun berechne einen Punkt der 156.5 %
pt += m_LightSourcePos; // von der Lichtquelle weg ist,
// in Richtung des Schnittpunktes
RenderGlow(0.8f, 0.5f, 0.1f, 0.5f, pt, 0.6f); // Rendere den kleinen Glow
pt = vLightSourceToIntersect * (Length * 1.0f); // Nun berechne einen Punkt der 200 %
pt += m_LightSourcePos; // von der Lichtquelle weg ist,
// in Richtung des Schnittpunktes
RenderHalo(0.5f, 0.5f, 0.7f, 0.5f, pt, 1.7f); // Rendere Halo
pt = vLightSourceToIntersect * (Length * 0.975f); // Nun berechne einen Punkt der 195 %
pt += m_LightSourcePos; // von der Lichtquelle weg ist,
// in Richtung des Schnittpunktes
RenderGlow(0.4f, 0.1f, 0.9f, 0.5f, pt, 2.0f); // Rendere den kleinen Glow
}
glDisable(GL_BLEND );
glEnable(GL_DEPTH_TEST);
glDisable(GL_TEXTURE_2D);
Es folgen die Funktionen RenderBigGlow, RenderStreaks, RenderGlow und RenderHalo. Die Funktionen sind identisch und unterscheiden sich nur in der Textur, die sie binden.
void glCamera::RenderHalo(GLfloat r, GLfloat g, GLfloat b, GLfloat a, glPoint p, GLfloat scale)
{
glPoint q[4];
// grundsätzlich machen wir nur eine 2D Box
// von vier Punkten brauchen wir keine Z Koordinate, weil
// wir die Kamera um die Inverse rotieren, so dass
// texturierte Quads immer zu uns zeigen.
q[0].x = (p.x - scale); // Setze die X Koordinate -scale Einheiten vom Mittelpunkt.
q[0].y = (p.y - scale); // Setze die Y Koordinate -scale Einheiten vom Mittelpunkt.
q[1].x = (p.x - scale); // Setze die X Koordinate -scale Einheiten vom Mittelpunkt.
q[1].y = (p.y + scale); // Setze die Y Koordinate scale Einheiten vom Mittelpunkt
q[2].x = (p.x + scale); // Setze die X Koordinate scale Einheiten vom Mittelpunkt
q[2].y = (p.y - scale); // Setze die Y Koordinate -scale Einheiten vom Mittelpunkt
q[3].x = (p.x + scale); // Setze die X Koordinate scale Einheiten vom Mittelpunkt
q[3].y = (p.y + scale); // Setze die Y Koordinate scale Einheiten vom Mittelpunkt
glPushMatrix(); // speicher die Modelview Matrix
glTranslatef(p.x, p.y, p.z); // translatiere zu unserem Punkt
glRotatef(-m_HeadingDegrees, 0.0f, 1.0f, 0.0f);
glRotatef(-m_PitchDegrees, 1.0f, 0.0f, 0.0f);
glBindTexture(GL_TEXTURE_2D, m_HaloTexture); // Binde die Halo Textur
glColor4f(r, g, b, a); // Setze die Farbe, da die Textur grau skaliert ist
glBegin(GL_TRIANGLE_STRIP); // zeichne Halo
glTexCoord2f(0.0f, 0.0f);
glVertex2f(q[0].x, q[0].y);
glTexCoord2f(0.0f, 1.0f);
glVertex2f(q[1].x, q[1].y);
glTexCoord2f(1.0f, 0.0f);
glVertex2f(q[2].x, q[2].y);
glTexCoord2f(1.0f, 1.0f);
glVertex2f(q[3].x, q[3].y);
glEnd();
glPopMatrix(); // stelle die Modelview Matrix wieder her
}
void glCamera::RenderGlow(GLfloat r, GLfloat g, GLfloat b, GLfloat a, glPoint p, GLfloat scale)
{
glPoint q[4];
// grundsätzlich machen wir nur eine 2D Box
// von vier Punkten brauchen wir keine Z Koordinate, weil
// wir die Kamera um die Inverse rotieren, so dass
// texturierte Quads immer zu uns zeigen..
q[0].x = (p.x - scale); // Setze die X Koordinate -scale Einheiten vom Mittelpunkt
q[0].y = (p.y - scale); // Setze die Y Koordinate -scale Einheiten vom Mittelpunkt
q[1].x = (p.x - scale); // Setze die X Koordinate -scale Einheiten vom Mittelpunkt
q[1].y = (p.y + scale); // Setze die Y Koordinate scale Einheiten vom Mittelpunkt
q[2].x = (p.x + scale); // Setze die X Koordinate scale Einheiten vom Mittelpunkt
q[2].y = (p.y - scale); // Setze die Y Koordinate -scale Einheiten vom Mittelpunkt
q[3].x = (p.x + scale); // Setze die X Koordinate scale Einheiten vom Mittelpunkt
q[3].y = (p.y + scale); // Setze die Y Koordinate scale Einheiten vom Mittelpunkt
glPushMatrix(); // speicher die Modelview Matrix
glTranslatef(p.x, p.y, p.z); // translatiere zu unserem Punkt
glRotatef(-m_HeadingDegrees, 0.0f, 1.0f, 0.0f);
glRotatef(-m_PitchDegrees, 1.0f, 0.0f, 0.0f);
glBindTexture(GL_TEXTURE_2D, m_GlowTexture); // Binde die Glow Textur
glColor4f(r, g, b, a); // Setze die Farbe, da die Textur grau skaliert ist
glBegin(GL_TRIANGLE_STRIP); // zeichne Glow
glTexCoord2f(0.0f, 0.0f);
glVertex2f(q[0].x, q[0].y);
glTexCoord2f(0.0f, 1.0f);
glVertex2f(q[1].x, q[1].y);
glTexCoord2f(1.0f, 0.0f);
glVertex2f(q[2].x, q[2].y);
glTexCoord2f(1.0f, 1.0f);
glVertex2f(q[3].x, q[3].y);
glEnd();
glPopMatrix(); // stelle die Modelview Matrix wieder her
}
void glCamera::RenderBigGlow(GLfloat r, GLfloat g, GLfloat b, GLfloat a, glPoint p, GLfloat scale)
{
glPoint q[4];
// grundsätzlich machen wir nur eine 2D Box
// von vier Punkten brauchen wir keine Z Koordinate, weil
// wir die Kamera um die Inverse rotieren, so dass
// texturierte Quads immer zu uns zeigen.
q[0].x = (p.x - scale); // Setze die X Koordinate -scale Einheiten vom Mittelpunkt
q[0].y = (p.y - scale); // Setze die Y Koordinate -scale Einheiten vom Mittelpunkt
q[1].x = (p.x - scale); // Setze die X Koordinate -scale Einheiten vom Mittelpunkt
q[1].y = (p.y + scale); // Setze die Y Koordinate scale Einheiten vom Mittelpunkt
q[2].x = (p.x + scale); // Setze die X Koordinate scale Einheiten vom Mittelpunkt
q[2].y = (p.y - scale); // Setze die Y Koordinate -scale Einheiten vom Mittelpunkt
q[3].x = (p.x + scale); // Setze die X Koordinate scale Einheiten vom Mittelpunkt
q[3].y = (p.y + scale); // Setze die Y Koordinate scale Einheiten vom Mittelpunkt
glPushMatrix(); // speicher die Modelview Matrix
glTranslatef(p.x, p.y, p.z); // translatiere zu unserem Punkt
glRotatef(-m_HeadingDegrees, 0.0f, 1.0f, 0.0f);
glRotatef(-m_PitchDegrees, 1.0f, 0.0f, 0.0f);
glBindTexture(GL_TEXTURE_2D, m_BigGlowTexture); // Bind To The Big Glow Texture
glColor4f(r, g, b, a); // Setze die Farbe, da die Textur grau skaliert ist
glBegin(GL_TRIANGLE_STRIP); // zeichne Big Glow
glTexCoord2f(0.0f, 0.0f);
glVertex2f(q[0].x, q[0].y);
glTexCoord2f(0.0f, 1.0f);
glVertex2f(q[1].x, q[1].y);
glTexCoord2f(1.0f, 0.0f);
glVertex2f(q[2].x, q[2].y);
glTexCoord2f(1.0f, 1.0f);
glVertex2f(q[3].x, q[3].y);
glEnd();
glPopMatrix(); // stelle die Modelview Matrix wieder her
}
void glCamera::RenderStreaks(GLfloat r, GLfloat g, GLfloat b, GLfloat a, glPoint p, GLfloat scale)
{
glPoint q[4];
// grundsätzlich machen wir nur eine 2D Box
// von vier Punkten brauchen wir keine Z Koordinate, weil
// wir die Kamera um die Inverse rotieren, so dass
// texturierte Quads immer zu uns zeigen.
q[0].x = (p.x - scale); // Setze die X Koordinate -scale Einheiten vom Mittelpunkt
q[0].y = (p.y - scale); // Setze die Y Koordinate -scale Einheiten vom Mittelpunkt
q[1].x = (p.x - scale); // Setze die X Koordinate -scale Einheiten vom Mittelpunkt
q[1].y = (p.y + scale); // Setze die Y Koordinate scale Einheiten vom Mittelpunkt
q[2].x = (p.x + scale); // Setze die X Koordinate scale Einheiten vom Mittelpunkt
q[2].y = (p.y - scale); // Setze die Y Koordinate -scale Einheiten vom Mittelpunkt
q[3].x = (p.x + scale); // Setze die X Koordinate scale Einheiten vom Mittelpunkt
q[3].y = (p.y + scale); // Setze die Y Koordinate scale Einheiten vom Mittelpunkt
glPushMatrix(); // speicher die Modelview Matrix
glTranslatef(p.x, p.y, p.z); // translatiere zu unserem Punkt
glRotatef(-m_HeadingDegrees, 0.0f, 1.0f, 0.0f);
glRotatef(-m_PitchDegrees, 1.0f, 0.0f, 0.0f);
glBindTexture(GL_TEXTURE_2D, m_StreakTexture); // Binde die Streak Textur
glColor4f(r, g, b, a); // Setze die Farbe, da die Textur grau skaliert ist
glBegin(GL_TRIANGLE_STRIP); // zeichne Streak
glTexCoord2f(0.0f, 0.0f);
glVertex2f(q[0].x, q[0].y);
glTexCoord2f(0.0f, 1.0f);
glVertex2f(q[1].x, q[1].y);
glTexCoord2f(1.0f, 0.0f);
glVertex2f(q[2].x, q[2].y);
glTexCoord2f(1.0f, 1.0f);
glVertex2f(q[3].x, q[3].y);
glEnd();
glPopMatrix(); // stelle die Modelview Matrix wieder her
}
Sie können die Tasten 'W', 'S', 'A' und 'D' benutzen, um die Richtung der Kamera zur ändern. Die Tasten '1' und '2' schaltet die Informationen ein / aus. 'Z' gibt der Kamera eine konstante Vorwärtsgeschwindigkeit. 'C' gibt der Kamera eine konstante 'Rückwärtsgeschwindigkeit' und 'X' stoppt die Kamerabewegung.
Das ist alles für dieses Tutorial. Alle Fragen, Kommentare und Beschwerden sind gerne gesehen. Nur auf meinen Namen unten klicken, um mir zu mailen. Natürlich bin ich nicht die erste Person die Lens Flares implementiert hat, deswegen folgen noch ein paar Links, die ich recht hilfreich fand, als ich dieses Tutorial geschrieben habe. Und bevor ich hier ende, möchte ich mich bei Dave Steere, Cameron Tidwell, Bert Sammons und Brannon Martindale für ihr Feedback und ihre Hilfe beim testen des Codes auf anderer Hardware, bedanken. Danke Jungs! Ich hoffe, dass Sie das Tutorial genossen haben.
Weitere Ressourcen:
http://www.gamedev.net/reference/articles/article874.asp
http://www.gamedev.net/reference/articles/article813.asp
http://www.opengl.org/developers/code/mjktips/lensflare/
http://www.markmorley.com/opengl/frustumculling.html
http://oss.sgi.com/projects/ogl-sample/registry/HP/occlusion_test.txt
http://oss.sgi.com/projects/ogl-sample/registry/NV/occlusion_query.txt
- Cheers
Vic Hollis
ANMERKUNGEN von Dario Corno a.k.a. rIO von Spinning Kids:
Ich habe einige Test eingefügt, um zu überprüfen, ob Objekte die Lens Flare verdecken. Dadurch wird die Flare ausgeschaltet, wenn ein Objekt sich davor befindet.
Der neue Code sollte gut kommentiert sein und wurde mit dem String # NEUER CODE # gekennzeichnet, so dass Sie nur nach diesem String suchen müssen, wenn Sie sich die Änderungen anschauen wollen.
Die Änderungen sind:
- Eine neue Funktion in der glCamera Klasse, names IsOccluded, die einen Boolean zurückgibt, wenn der Parameter Punkt hinter einem Objekt ist
- Einige neue Variablen, um den gluCylinder zu speichern (der zum verdecken benutzt wird)
- Etwas neuer Zeichnen-Code in glDraw, um das Verdeckungs-Objekt zu zeichnen
- Etwas neuer Aufräum-Code, um den Quadric des Zylinders freizugeben
Das ist alles, ich hoffe Sie finden die veränderte Version interessant!
P.S: Etwas als Hausaufgabe... Es wäre gut, mehr als einen Punkt in der Nähe der Flare Position zu machen, um einen Fade zu realisieren, anstatt es einfach verschwinden zu lassen.
* DOWNLOAD Visual C++ Code für diese Lektion.
* DOWNLOAD Borland C++ Builder 6 Code für diese Lektion. ( Conversion by Le Thanh Cong )
* DOWNLOAD Delphi Code für diese Lektion. ( Conversion by Michal Tucek )
* DOWNLOAD Dev C++ Code für diese Lektion. ( Conversion by Michael Small )
* DOWNLOAD Code Warrior 5.3 Code für diese Lektion. ( Conversion by Scott Lupton )
* DOWNLOAD Python Code für diese Lektion. ( Conversion by Brian Leair )
* DOWNLOAD Visual Studio .NET Code für diese Lektion. ( Conversion by Joachim Rohde )
* DOWNLOAD Lesson 44 - mit Extension Unterstützung (VC++).
Deutsche Übersetzung: Joachim Rohde
Der original Text ist hier zu finden.
Die original OpenGL Tutorials stammen von NeHe's Seite.




